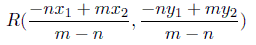ベクトルの内積 (Inner product)

公式

C言語での実装

#include <stdio.h>

/* ---------------------------------------------
  ベクトルの内積を求める
  引数1: vec1 ベクトル1
  引数2: vec2 ベクトル2
  引数3: n ベクトルの要素数
  戻り値 ベクトルの内積
 ---------------------------------------------*/
double inner_product(double *vec1, double *vec2, int n) {
    int i;
    double s = 0.0;

    for ( i = 0; i < n; i++ ) {
        s += vec1[i] * vec2[i];
    }

    return s;
}

/* main */
int main(void)
{
    double a[] = {1.0, 2.0, 3.0};
    double b[] = {2.0, 3.0, 4.0};
    int n = 3;

    /* ベクトルの内積を求める */
    printf("内積: %.2f\n", inner_product(a, b, n));

    return 0;
}

実行例

内積: 20.00

ベクトルの長さ

公式

C言語での実装

#include <stdio.h>
#include <math.h>

/* ---------------------------------------------
  ベクトルの長さを求める
  引数1: vec ベクトル
  引数4: n ベクトルの要素数
  戻り値 vecの長さ
 ---------------------------------------------*/
double norm(double *vec, int n)
{
    int i;
    double s = 0.0;

    for ( i = 0; i < n; i++ ) {
        s += vec[i] * vec[i];
    }

    return sqrt(s);
}

/* main */
int main(void)
{
    double vec[] = {1.0, 2.0, 3.0};
    int n = 3;

    /* ベクトルの長さを求める */
    printf("ベクトルの長さ: %f\n", norm(vec, n));

    return 0;
}

実行例

ベクトルの長さ: 3.741657

ベクトルの差

公式

C言語での実装

#include <stdio.h>

/* ---------------------------------------------
  ベクトルの和を計算する
  引数1: vec1 ベクトル1
  引数2: vec2 ベクトル2
  引数3: sum ベクトルの和
  引数4: n ベクトルの要素数
  戻り値 sumの先頭アドレス
 ---------------------------------------------*/
double *diff_vector(double *vec1,
        double *vec2, double *diff, int n)
{
    while (n--)
        diff[n] = vec1[n] - vec2[n];
    return diff;
}

/* main */
int main(void)
{
    double vec1[] = {1.0, 2.0, 3.0};
    double vec2[] = {2.0, 4.0, 1.0};
    double diff[3];
    int i, n = 3;

    /* ベクトルの差を計算 */
    diff_vector(vec1, vec2, diff, n);

    for ( i = 0; i < n; i++ ) {
        printf("diff[%d] = %.2f\n", i, diff[i]);
    }

    return 0;
}

実行例

diff[0] = -1.00
diff[1] = -2.00
diff[2] = 2.00

ベクトルの和

公式

C言語での実装

#include <stdio.h>

/* ---------------------------------------------
  ベクトルの和を計算する
  引数1: vec1 ベクトル1
  引数2: vec2 ベクトル2
  引数3: sum ベクトルの和
  引数4: n ベクトルの要素数
  戻り値 sumの先頭アドレス
 ---------------------------------------------*/
double *sum_vector(double *vec1,
        double *vec2, double *sum, int n)
{
    while (n--)
        sum[n] = vec1[n] + vec2[n];
    return sum;
}

/* main */
int main(void)
{
    double vec1[] = {1.0, 2.0, 3.0};
    double vec2[] = {2.0, 4.0, 1.0};
    double sum[3];
    int i, n = 3;

    /* ベクトルの和を計算 */
    sum_vector(vec1, vec2, sum, n);

    for ( i = 0; i < n; i++ ) {
        printf("sum[%d] = %.2f\n", i, sum[i]);
    }

    return 0;
}

実行例

sum[0] = 3.00
sum[1] = 6.00
sum[2] = 4.00

三角形の重心(Triangle’s center of gravity)

公式

A(x1, y1)，B(x2, y2),C(x3, y3)のとき△ABCの重心Gの座標は

C言語での実装

#include <stdio.h>
#include <math.h>

/* ---------------------------------------------
   3点A,B,Cからなる三角形の重心を求める (2次元)
   引数1: A 点の座標1
   引数2: B 点の座標2
   引数3: C 点の座標3
   引数5: G 重心
   戻り値: 重心の先頭アドレス
 ---------------------------------------------*/
double *triangle_center_of_gravity(double A[2],
        double B[2], double C[2], double G[2])
{
    G[0] = (A[0] + B[0] + C[0]) / 3.0;
    G[1] = (A[1] + B[1] + C[1]) / 3.0;
    return G;
}

/* main */
int main(void)
{
    double A[] = {0.0, 1.0};
    double B[] = {-1.0, 0.0};
    double C[] = {1.0, 0.0};
    double G[2];

    triangle_center_of_gravity(A, B, C, G);
    printf("3点A,B,Cからなる三角形の重心G(%.2f, %.2f)\n",
        G[0], G[1]);

    return 0;
}

実行例

3点A,B,Cからなる三角形の重心G(0.00, 0.33)

外分点(externally dividing point)

公式

2点 P(x1, y1)，Q(x2, y2)について、線分PQをm:nに外分する点Rは

C言語での実装

#include <stdio.h>
#include <math.h>

/* ---------------------------------------------
   2点p1,p2からなる線分をm:nに外分する点を求める (2次元)
   引数1: P 点の座標1
   引数2: Q 点の座標2
   引数3: m m:nのm
   引数4: n m:nのn
   引数5: result 外分点
   戻り値: 1 正常終了，0 異常終了
 ---------------------------------------------*/
int divide_externally_2D(double P[2],
        double Q[2], int m, int n, double R[2])
{
    if (m - n == 0) return 0;

    R[0] = (-n * P[0] + m * Q[0]) / (m - n);
    R[1] = (-n * P[1] + m * Q[1]) / (m - n);

    return 1;
}

/* main */
int main(void)
{
    double P[] = {1.0, 3.0};
    double Q[] = {2.0, 4.0};
    double R[2];
    int m = 2;
    int n = 3;

    divide_externally_2D(P, Q, m, n, R);
    printf("線分PQを%d:%dに外分する点R(%.2f, %.2f)\n", 
        m, n, R[0], R[1]);

    return 0;
}

実行例

2点P,Qからなる線分を2:3に外分する点R(-1.00, 1.00)

内分点 (internally dividing point)

公式

2点 P(x1, y1)，Q(x2, y2)について、線分PQをm:nに内分する点Rは

C言語での実装

#include <stdio.h>
#include <math.h>
/* ---------------------------------------------
   2点P,Qからなる線分をm:nに内分する点を求める (2次元)
   引数1: P 点の座標1
   引数2: Q 点の座標2
   引数3: m m:nのm
   引数4: n m:nのn
   引数5: result 内分点
   戻り値: 1 正常終了，0 異常終了
 ---------------------------------------------*/
int divide_internally_2D(double P[2], 
        double Q[2], int m, int n, double R[2])
{
    if (m < 1 && n < 1) return 0;

    R[0] = (n * P[0] + m * Q[0]) / (m + n);
    R[1] = (n * P[1] + m * Q[1]) / (m + n);

    return 1;
}

/* main */
int main(void)
{
    double P[] = {1.0, 3.0};
    double Q[] = {2.0, 4.0};
    double R[2];
    int m = 2;
    int n = 3;

    divide_internally_2D(P, Q, m, n, R);
    printf("線分PQを%d:%dに内分する点R(%.2f, %.2f)\n", 
        m, n, R[0], R[1]);

    return 0;
}

実行例

線分PQをを2:3に内分する点R(1.40, 3.40)